直线型边关系、角关系、边角互化相关定理

一些约定：

在 $\triangle ABC$ 中， $BC=a,AC=b,AB=c.\angle BAC=A,\angle ABC=B,\angle BCA=C,p=\dfrac12(a+b+c),$

内切圆半径 $r=\sqrt{\dfrac{(p-a)(p-b)(p-c)}{p}}$ ，外接圆半径 $R=\dfrac{abc}{4\sqrt{p(p-a)(p-b)(p-c)}},$

面积 $S=\dfrac12ab\sin C=\dfrac12ac\sin B=\dfrac12bc\sin A=\sqrt{p(p-a)(p-b)(p-c)}=rp$

一、共点共线结论

Menelaus 定理

如图，设 $A'、B'、C'$ 分别是 $\triangle ABC$ 的三边 $BC、CA、AB$ 所在直线上的点，点 $O$ 不在 $\triangle ABC$ 三边所在直线上，若 $A'、B'、C'$ 共线（截线），则有：

边关系： $\dfrac{BA'}{A'C}\cdot\dfrac{CB'}{B'A}\cdot\dfrac{AC'}{C'B}=1$ ，

角关系：第一角元形式：$\dfrac{\sin \angle BAA'}{\sin\angle A'AC}\cdot\dfrac{\sin \angle ACC'}{\sin\angle C'CB}\cdot\dfrac{\sin\angle CBB'}{\sin\angle B'BA}=1$ ，

​ 第二角元形式：$\dfrac{\sin \angle BOA'}{\sin\angle A'OC}\cdot\dfrac{\sin \angle COB'}{\sin\angle B'OA}\cdot\dfrac{\sin\angle AOC'}{\sin\angle C'OB}=1$ 。

证明：

对于边关系，过一顶点作对边平行线与截线相交，通过平行线分线段成比例定理转移即得。

对于第一角元形式，有 $\dfrac{BA'}{A'C}=\dfrac{S_{\triangle ABA'}}{S_{\triangle ACA'}}=\dfrac{\frac12AB\cdot AA'\cdot \sin\angle BAA'}{\frac12AC\cdot AA'\cdot \sin\angle CAA'}=\dfrac{AB\cdot\sin \angle BAA'}{AC\cdot\sin \angle CAA'}$ ，其余两项同理，代入即得。

对于第二角元形式，有 $\dfrac{S_{\triangle BOA'}}{S_{\triangle COA'}}=\dfrac{BA'}{A'C}$ ，故有 $\dfrac{\sin\angle BOA'}{\sin\angle A'OC}=\dfrac{OC}{OB}\cdot\dfrac{BA'}{A'C}$ ，其余两项同理，代入即得。

它的逆命题也成立。

推论：Desargues 定理

如图，若两三角形对应点连线交于一点，则其对应边交点共线。

证明：三组梅涅劳斯证一下即可。

Ceva 定理

设 $A'、B'、C' $ 分别是 $\triangle ABC$ 的三边 $BC，CA，AB$ 或其延长线上的点，点 $O$ 不在 $\triangle ABC$ 的三边及其延长线上，若 $AA'，BB'，CC'$ 三线平行或共点，则有：

边关系： $\dfrac{BA'}{A'C}\cdot\dfrac{CB'}{B'A}\cdot\dfrac{AC'}{C'B}=1$ ，

角关系：第一角元形式：$\dfrac{\sin\angle BAA'}{\sin\angle CAA'}\cdot\dfrac{\sin\angle ACC'}{\sin\angle BCC'}\cdot\dfrac{\sin\angle CBB'}{\sin\angle ABB'}=1$ ，

​ 第二角元形式：$\dfrac{\sin\angle BOA'}{\sin\angle COA'}\cdot\dfrac{\sin\angle AOC'}{\sin\angle BOC'}\cdot\dfrac{\sin\angle COB'}{\sin\angle AOB'}=1$ 。

证明：类似 Menelaus 定理。

它的逆命题也成立。

二、三角形一顶点引出一射线相关结论

张角定理

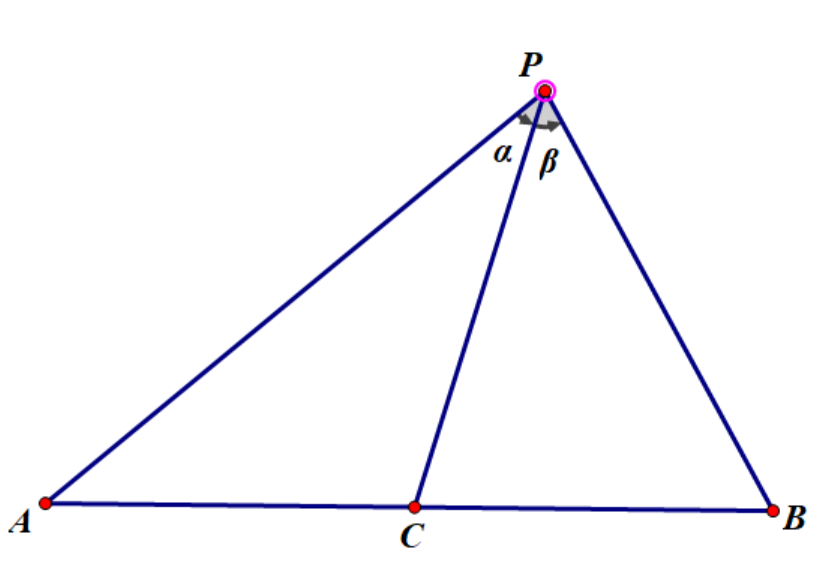
如图，在 $\triangle ABP$ 中 $C$ 是 $AB$ 上一点，$\angle APC=\alpha，\angle BPC=\beta$ ，则有：

边角互化： $\dfrac{\sin(\alpha+\beta)}{PC}=\dfrac{\sin \alpha}{PB}+\dfrac{\sin \beta}{PA}$ 。

证明： $S_{\triangle ABP}=S_{\triangle ACP}+S_{\triangle CBP}$ ，然后把三个面积表示为形如 $\frac12ab\sin C$ 的形式，两边同除 $PA\cdot PB\cdot PC$ ，即得。

它的逆命题也成立。

Stewart 定理

设 $P$ 为 $\triangle ABC$ 的 $BC$ 上异于 $B、C$ 任意一点，则有：

边关系：$AB^2\cdot PC+AC^2\cdot BP-AP^2\cdot BC=BP\cdot PC\cdot BC$ 。

证明： $\cos\angle APB，\cos\angle APC$ 用两个余弦定理即得。

它的逆命题也成立。

推论：

中线公式：当 $P$ 为 $BC$ 中点时，$AP=\dfrac12\sqrt{2(b^2+c^2)-a^2}$ ，

角平分线长公式：当 $AP$ 为 $\angle A$ 的角平分线时，$AP=\dfrac2{b+c}\sqrt{bcp(p-a)}=AB\cdot AC-BD\cdot CD$ ，

（不是由它推出的）高线长公式：当 $AP\bot BC$ 时，$AP=\dfrac{2\sqrt{p(p-a)(p-b)(p-c)}}a$ 。

证明：代入化简即得。

三、解三角形

正弦定理

$\dfrac a{\sin A}=\dfrac b{\sin B}=\dfrac c{\sin C}=2R$

余弦定理

$\cos A=\dfrac{b^2+c^2-a^2}{2bc},\cos B=\dfrac{a^2+c^2-b^2}{2ac},\cos C=\dfrac{a^2+b^2-c^2}{2ab}$

射影定理

$a=b\cos C+c\cos B,b=a\cos C+c\cos A,C=a\cos B+b\cos A$

tricks